Flusso magnetico e densità di flusso magnetico
Che cosa sono il flusso magnetico e la densità di flusso magnetico?
Il flusso magnetico è la densità di flusso magnetico che attraversa una superficie immaginaria. La densità di flusso magnetico si riferisce alla densità delle linee di campo. Quanto più dense sono le linee di campo, tanto maggiore è la densità del flusso magnetico. Poiché, secondo le leggi fisiche dell'elettrodinamica, le equazioni di Maxwell, nessuna linea di campo può semplicemente fermarsi, la densità di flusso continua a passare dal magnete allo spazio esterno.Indice
Cosa indicano il flusso magnetico e la densità di flusso magnetico?
Il flusso magnetico Φ può essere inteso come l'insieme di tutte le linee di campo magnetico. La densità di flusso magnetico B descrive la densità e la direzione delle linee di campo che passano attraverso una superficie immaginaria nello spazio. Se le linee di campo corrono in linea retta (ad esempio tra i poli di un magnete a ferro di cavallo), allora il flusso magnetico Φ attraverso una certa area A, che è perpendicolare al flusso, è il prodotto della densità di flusso magnetico B e dell'area A: Φ = B•AIndirettamente, la densità di flusso magnetico (campo B) è anche una misura dell'intensità del campo magnetico. Tuttavia, non è del tutto corretto riferirsi al campo B come a un campo magnetico, anche se ciò si trova occasionalmente in letteratura. Il campo magnetico è solitamente abbreviato con la lettera H e si applica la relazione B=μ0 μ•H con la costante di permeabilità magnetica del vuoto µ0 e una costante di permeabilità magnetica specifica del materiale µ. Tuttavia, di solito è circa 1, tranne che per i materiali ferromagnetici, per i quali µ può assumere valori fino a 100 000, e per i superconduttori con µ=0. Il prodotto di µ,µ0 e del campo magnetico H dà il campo B, cioè la densità del flusso magnetico B.
La densità di flusso magnetico si misura in Tesla (T). Il flusso magnetico si misura in Tm². L'unità 1 Tm² è anche indicata come 1 Weber (Wb).
La rimanenza di un materiale magnetizzato descrive la densità di flusso magnetico che si sprigiona dal materiale dopo la magnetizzazione. Viene anche specificata in Tesla.
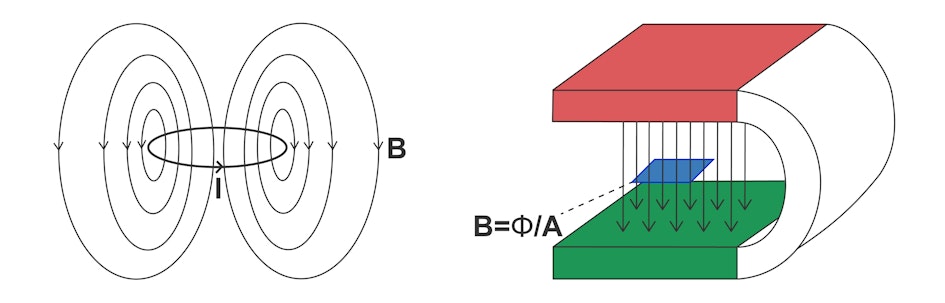
Figura: una corrente I
causa sempre una densità di flusso magnetico B
.
Un flusso magnetico proviene da una corrente circolare che circonda la spira del conduttore nel modo illustrato.
Le linee di campo sono disegnate in modo schematico.
In realtà, il flusso magnetico riempie l'intero spazio e le linee di campo sono sempre chiuse nel loro insieme.
Esse corrono nello spazio esterno dal polo nord al polo sud e poi attraverso l'anello conduttore dal polo sud al polo nord.
Nel magnete a ferro di cavallo (lato destro, polo nord rosso, polo sud verde), le linee di campo tornano al polo nord all'interno del materiale.
Per l'andamento delle linee di campo è irrilevante che si parli di densità di flusso magnetico B
o di campo magnetico H,
poiché entrambi sono proporzionali tra loro.
Vale la relazione B=μ0μ•H.
Come mostrato sul lato destro, la densità di flusso magnetico è la proporzione del flusso magnetico Φ
per l'area A
(in blu).
B
è quindi proporzionale al numero di linee di campo che passano attraverso una superficie immaginaria.
Correnti come causa
Il flusso magnetico è causato dalle correnti, cioè dal movimento di cariche. Le correnti creano solo linee di campo chiuse. Il flusso magnetico non ha quindi né inizio né fine. Dal punto di vista fisico, si dice anche che non esistono fonti e pozzi di densità di flusso magnetico e flusso magnetico.Questo è il motivo per cui un magnete deve sempre avere due poli. Un polo nord e un polo sud. Matematicamente, ciò è espresso dalle equazioni di Maxwell. Un tipico magnete a corrente è l'elettromagnete.
Anche nei magneti permanenti, le microscopiche correnti circolari I, ossia i movimenti degli elettroni nel materiale, sono responsabili del flusso magnetico e quindi anche del campo magnetico. Queste correnti circolari provocano un flusso magnetico B, che emerge dalla corrente circolare (anello di corrente), percorre un arco verso la parte inferiore dell'anello di corrente e vi si richiude (vedi figura). La corrente circolare crea un momento magnetico con il polo nord sopra la spira e il polo sud sotto la spira. Se il senso della corrente viene invertito, anche i poli nord e sud si scambiano.
Determinare il flusso magnetico
Di conseguenza, il flusso magnetico è fisicamente definito dal suo effetto induttivo su una spira di conduttore. Se una spira di conduttore di area nota viene posta in un campo magnetico, viene indotta una sovratensione. L'integrale temporale di questo picco di tensione è uguale al flusso magnetico Φ:\(\int{U_{ind}dt}=B\cdot{A}=\Phi\)
Il flusso magnetico può quindi essere misurato anche utilizzando una spira di conduttore e la tensione indotta in questa spira di conduttore. Tuttavia, a questo scopo si utilizza solitamente una più precisa sonda di Hall.
Determinare la densità di flusso magnetico
Se consideriamo la densità di flusso magnetico B, che attraversa una superficie curva, il flusso magnetico deve essere determinato come l'integrale della densità di flusso vettoriale sulla normale alla superficie:\(\int{\vec{B}d\vec{A}}=\Phi\)
Poiché le linee di campo sono chiuse, tutte le linee di campo che passano attraverso una superficie chiusa (ad esempio un guscio sferico) devono passare anche all'interno della sfera e viceversa. In termini matematici, ciò significa che il flusso attraverso le superfici chiuse è sempre nullo e, di conseguenza, non esistono sorgenti o pozzi di densità di flusso magnetico:
\(\oint_{A-geschlossen}{\vec{B}d\vec{A}}=0 \Leftrightarrow \vec{\nabla}\cdot{\vec{B}}=0\)
Ciò equivale alla cosiddetta libertà dalla divergenza della densità di flusso magnetico, come affermato da una delle quattro equazioni di Maxwell.
Nella nostra sezione FAQ troverete una tabella in formato Excel o OpenOffice che potrete utilizzare per calcolare comodamente la densità di flusso dei magneti.

Autore:
Dott. Franz-Josef Schmitt
Il dottor Franz-Josef Schmitt è fisico e direttore scientifico del corso pratico avanzato di fisica all'università Martin-Luther di Halle-Wittenberg. Ha lavorato alla Technische Universität di Berlino dal 2011 al 2019, dove ha diretto diversi progetti pedagogici e il laboratorio di progetti di chimica. Le sue ricerche si concentrano sulla spettroscopia di fluorescenza risolta nel tempo su macromolecole biologicamente attive. Inoltre è il direttore di Sensoik Technologies GmbH.
Dott. Franz-Josef Schmitt
Il dottor Franz-Josef Schmitt è fisico e direttore scientifico del corso pratico avanzato di fisica all'università Martin-Luther di Halle-Wittenberg. Ha lavorato alla Technische Universität di Berlino dal 2011 al 2019, dove ha diretto diversi progetti pedagogici e il laboratorio di progetti di chimica. Le sue ricerche si concentrano sulla spettroscopia di fluorescenza risolta nel tempo su macromolecole biologicamente attive. Inoltre è il direttore di Sensoik Technologies GmbH.
Il diritto d'autore sull'intero contenuto del compendio (testi, foto, illustrazioni ecc.) appartiene all'autore Franz-Josef Schmitt. I diritti esclusivi di utilizzazione dell'opera appartengono a Webcraft GmbH, Svizzera (come gestore di supermagnete.de). Senza espressa autorizzazione di Webcraft GmbH non è permesso copiarne il contenuto né utilizzarlo in alcun'altra forma. Proposte di miglioramento o complimenti riguardo al compendio possono essere inviati per e-mail a
[email protected]
© 2008-2025 Webcraft GmbH
© 2008-2025 Webcraft GmbH
